Donde salta la liebre
«Quien tropieza, a aprender empieza». Refrán popular
Los refranes son expresiones breves y concisas, de origen y uso popular que transmiten enseñanzas o consejos prácticos basados en la experiencia colectiva y lo hacen con una esencial carga de creatividad, humor, sarcasmo e inteligencia.
Donde menos se espera salta la liebre, alude a los sucesos que se presentan de forma repentina o inesperada, llenando de sobresalto el sentir de las personas. Y eso me sucede con frecuencia en el quehacer matemático, donde tropiezo a cada momento con formas o comportamientos que parecen salidos de un acto de magia.
Hacer matemáticas es en esencia descubrir formas o comportamientos presentes en los entes matemáticos o en sus relaciones, es una actividad que estimula, entre otras cosas, la atención, la observación y el análisis, tres valores importantes en la vida.
Por mi inclinación matemática me resulta natural encontrarme con mucha frecuencia en los hoy populares medios de comunicación, publicaciones donde se presentan formas matemáticas que provocan comentarios de asombro y admiración. Y debo decir que los disfruto.
Mi apetencia por las matemáticas y de manera especial por el redescubrimiento de formas o comportamientos como accionespropias de esta disciplina, hacen que ante cualquier compromiso matemático tienda a ir en la búsqueda de esa mágica esencia. Y, al redescubrirla, me lleno de una indescriptible alegría.
Pues bien, hace unos días, una publicación retaba a encontrar el resultado de la siguiente operación:
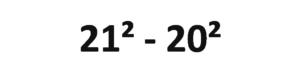
A todas luces el reto no mostraba dificultad alguna: 21² = 21 x 21 = 441, y 20² = 20 x 20 =400, por lo tanto,21² – 20² = 441 – 400 = 41.Pero, en mi mente surgió la idea de que el proponente quizás pretendía suscitar alguna forma que permitiese una rápida y precisa solución. Y aquí es donde ¡saltó la liebre! Me dispuse a jugar al matemático y vinieron las deducciones.
- Si multiplico por sí mismo un número que termina en cero, entonces el producto terminará en cero.
- Si multiplico por sí mismo un número que termina en uno, entonces el producto terminará en uno.
- Por lo tanto, el resultado de esa operación propuesta u otras similares, terminarán siempre en uno.
Estas conclusiones pueden verse como intrascendentes, pero orientan en el resultado a obtener y ello es ya una ayuda. Mas, ahora viene lo imprevisto, pero si sospechado.
¿Qué sucede si trabajo con otras parejas de números (al cuadrado)
terminados en uno y cero?
(10 y 11) – (31 y 30) – (41 y 40), …
La tabla adjunta muestra los resultados:
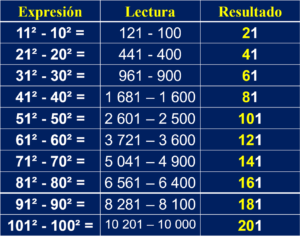
Además de que todas las sustracciones terminan en 1, la expresión resultante va aumentando de 2 en 2 en los valores anteriores al uno (en amarillo: 2,4, 6, 8, 10, 12, 14, 16, 18, 20, …). Ello avisa de la presencia de una forma, y ahí estaba, mostrándoseme:
(**)Los resultados de las sustracciones siempre son la suma de las bases de las potencias
Dicha forma permite obtener resultados rápidos y precisos de otras sustracciones con valores similares:
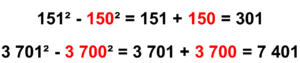
Y así es como me entretengo y ejercito, en lo que denomino,“matemaloquiando”(*), es decir, jugando al matemático, redescubriendo formas, esos comportamientos mágicos del cual está llena esta disciplina del conocimiento.
Cuando concluía de escribir este artículo mi teléfono anuncia la presencia de otro reto matemático.
Determinar el resultado de:
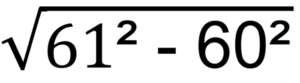
Entonces duplico 60, alcanzando120 y le sumo 1, obteniendo121 y la raíz de 121 es 11; y así confirmo el refrán (un tanto modificado) que dicta…
“Más vale maña, que esfuerzo”.
(*) Mateloquiando es un término que empleo como título de una serie de programas que estoy publicando en Matemalandia, canal personal en YouTube. Los programas, que tienen mi particular enfoque, están saliendo con el título de “Mateloquiando con…
(**) Para los que tienen formación matemática y en atención a que, en Matemática algo es verdad hasta que se demuestre, es claro que:
(10N + 1)² – (10N)² = 100N² + (2x10N + 1)– 100N² = (10N + 1) + 10N
Por ello doy por demostrada y válida la forma propuesta.



