Mario Arguedas, educador jubilado.
Cuando las leyes de la Matemática se refieren a la realidad, no son ciertas;cuando son ciertas, no se refieren a la realidad. Albert Einstein.
Veinte personas sentadas en un aula que cuenta con20 sillas (una para cada persona), podrán sentarse (ocupar posiciones diferentes)de 2₃ 432 902₂ 008 176₁ 640 000(dos trillones, 432 mil novecientos dos billones, 8 mil ciento setenta y seismillones, 640 mil) formas diferentes.
¿Cómo se logra establecer dicho cálculo?
En la práctica diaria, si procediésemos a realizar todos esos movimientos con una rapidez de un segundo cada cambio, requeriríamos de un tiempo aproximado de77146₁816 600años.
Tómese en consideración que la edad del universo es de 13 800 millones de años (13 800₁ 000 000), la vida comenzó en la Tierra hace al menos 3.5 mil millones de años(3 500₁ 000 000) y la especie humana moderna (Homo Sapiens) surgió en África hace 200 000años.
Ante tales evidencias, tratar de demostrar en la práctica que el dato ofrecido es correctoresulta más que imposible. Entonces emerge la Matemática con sus formas y nos lo explica.
Iniciemos con lo básico. Para ello denominemos a las personas con las letras del abecedario: A,B,C,D,…Veamos los cuatro primeros casos:
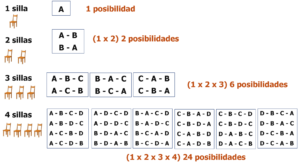
Como puede observarse las posibilidades de ocupar posiciones diferentes con N sillas,viene dada por el producto de todos los enteros positivos menores o iguales queN.

En la práctica, a partir de cinco sillas ya resulta laborioso determinar todas las posibilidades, luego, para 20es más que imposible:
1 x 2 x 3 x 4 x 5 x … x 20 = 2₃ 432 902₂ 008 176₁ 640 000
A esta forma se le conoce con el nombre defactorial de un número; si el número es n, su factorial se identificacomo n!y se lee ene factorial, en cuyo caso sería el producto de todos los enteros positivos menores o iguales que n.
8! = 1 x 2 x 3 x 4 x 5 x 6 x 7 x 8 = 40 320 (ocho factorial)
10! = 1 x 2 x 3 x 4 x 5 x 6 x 7 x 8 x 9 x 10 = 3₁628 800 (diez factorial)

Lamentalista calculadora, astróloga y escritora IndiaShakuntalaDevi (1929-2139)sentencia que “los números tienen vida, no son símbolos en un papel”, ello nos permite deducir que el propósito de la Matemática es la comprensión, no los números; no se leen números como tampoco se leen palabras, se leen significados.



