La geometría es el lenguaje universal de las formas, sin palabras.
Los griegos gozaron su interés por la Geometría a tal grado de querer explicar muchas de las cosas por su medio, como fue el caso de ciertos comportamientos numéricos.
Algunas de esas relaciones quedan aún hoy como pequeños vestigios de dicha época, mostrándose en los aprendizajes matemáticos más como un lenguaje y no tanto por su esencia, su razón. Expresiones como elevar al cuadrado al cubo, o sus inversas, extraer raíz cuadrada o cúbica, nos hablan de ello (*).
El término elevar al cuadrado se utiliza para referir a elevar un número al exponente “2” y la razónde ello se encuentra en que la secuencia de números al cuadrado toma la forma del área (número de cuadraditos) de superficies cuadradas:
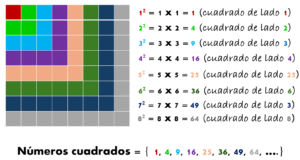
Explicando el concepto de operación inversa (radicalización), los lados de cada cuadrado corresponden a las raíces pares positivas de dichos cuadrados, así las cosas:
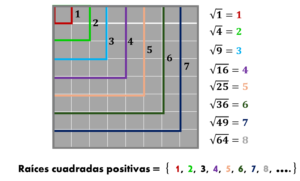
Si observa con detenimiento se dará cuenta que los valores cuadrados se forman por la suma consecutiva de números impares, denominados por los griegos como números gnomon o escuadra (términos en desuso):

Como se puede ver, los números cuadrados resultan de la suma de un cuadrado y un gnomon o escuadra (impar).
Otra variedad de números son los triangulares, denominados así por dibujar triángulos equiláteros (lados de igual medida).
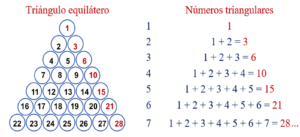
Números triangulares = {1, 3, 6, 10, 15, 21, 28, …}
Los números triangulares son el resultado de la suma sucesiva de números enteros (positivos), a los cuales Gauss (a la edad de 10 años) les descubrió una forma o comportamiento algebraico descrito así:

Los números toman cuerpo
Los matemáticos griegos fueron más allá y dotaron de cuerpo a los números, así por ejemplo dispusieron los números cúbicos como aquellos números positivos que resultaban de elevar a un exponente tres, haciendo corresponder el respectivo volumen (número de cubitos que lo forman):
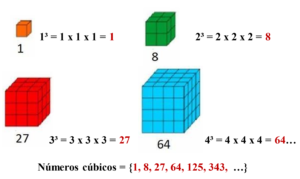
De manera consecuente, la raíz cúbica, como operación inversa de elevar al cubo, está dada por la medida de la arista del cubo.
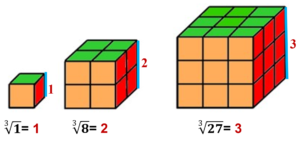
Las formas cuadradas y cúbicas posiblemente han permanecido en el argot matemático por ser valores de uso frecuente, sobre todo a nivel escolar. Otras construcciones perdieron su mención con el tiempo y hoy sirven como medios de motivación en las aulas de profesores caprichosos. Tal es el caso de los números piramidales cuadrangulares.

Esta clase de números resultan de la suma de números cuadrados consecutivos y dibujan pirámides cuadrangulares (base cuadrada) de lado 1, 2, 3, 4, …, y así sucesivamente.
Son diversas las asociaciones efectuadas por los matemáticos griegos de la Geometría a la Aritmética, donde la hermana mayor funge como herramienta que dota deformas (dibujos o figuras) a los números. Pero, en siglo XVI –XVII, los matemáticos invirtieron la relación y se dedicaron a asociar el Álgebra (generalización de la Aritmética) con la Geometría, permitiendo que las figuras geométricas fuesen interpretadas como expresiones algebraicas, dando así nacimiento a una rama conocida como Geometría Analítica, fuente de nuevo conocimiento matemático. Ello será tema de un próximoartículo.
(*) Es pertinente aclarar que los griegos establecieron las relaciones numérico-geométricas, dando nombre a las relaciones numéricas aquí expuestas, pero, muchos de los términos se replantearon cientos de años después, al emerger nuevo conocimiento. Los conceptos de potencias y raíces, por ejemplo, emergieron muchos años después.