Mario Arguedas, profesor de Matemáticas jubilado.
«Todas las verdades de las matemáticas están vinculadas entre sí». Adrien-Marie Legendre, (matemático: 1752 – 1833).
Un cuadrilátero es un polígono que tiene cuatro lados y como me propongo explicar, la determinación del área correspondiente a cualquiera de ellos se fundamenta en la forma del área de la superficie rectangular.
Iniciemos analizando los cuadriláteros que son paralelogramos, es decir, que tienen dos parejas de lados paralelos.

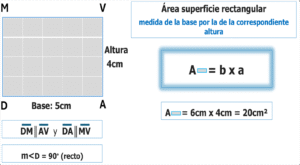
Es un cuadrilátero con dos parejas de lados paralelos. El rectángulo cumple con ese requisito, por lo tanto, el rectángulo es un paralelogramodonde uno de sus ángulos internos es recto (por consecuencia los otros tres también).

Luego el área de toda superficie correspondiente a un paralelogramo es el producto de la medida de la base por la altura.

Es un paralelogramo con un ángulo interno recto (por consecuencia los otros tres también) y lados congruentes (de igual medida). Por definición todo cuadrado es un rectángulo (rectángulo de lados congruentes); por lo tanto, el área correspondiente a su superficie tiene el mismo comportamiento que el de superficies rectangulares.
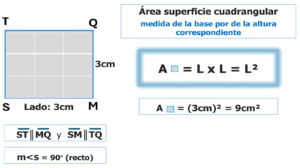
El área de la superficie cuadradatambién es el producto de las medidas de la base por la de la altura, pero al tener lados congruentes (de igual medida), entonces el área es igual a la medida de uno de sus lados elevado al cuadrado.

Es un paralelogramo cuyos lados son congruentes. La definición nos permite deducir que todo cuadrado es rombo, pero no todo rombo es cuadrado. Dicho de otro modo, el cuadrado es un rombo con un ángulo interno recto (por consecuencia los otros tres también).
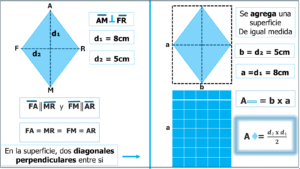
El área de la superficie rombal también es el producto de las medidas de la base (diagonal 2) por la de la altura (diagonal 1), pero dividido por dos porque se agregó una superficie igual para formar la superficie rectangular.
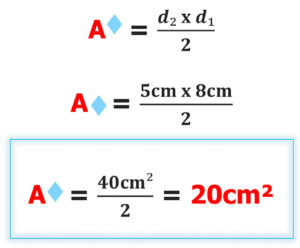
Como puede deducirse, todas las áreas de las superficies correspondientes a los paralelogramos se fundamentan en la correspondiente área de la superficie rectangular.



