Mario Arguedas, profesor pensionado.
«Dios puede que no juegue a los dados con el universo, pero algo extraño está pasando con los números primos».
Paul Erdos, Matemático Húngaro (1913-1996).
La frase “Dios no juega a los dados” atribuida al físico Albert Einstein, es una metáfora que plantea el hecho de que Dios no toma decisiones aleatorias o al azar, que existe un orden e intención en la creación y forma de funcionar el universo. Por lo tanto, cuando Erdos advierte que “algo extraño está pasando con los números primos” lo que sugiere es que conviene prestarle atención al comportamiento casual mostrado por esta clase de números.
Un número natural es primo si tiene exactamente dos divisores, caso del3 (solo divisible por 1 y por sí mismo). El 1 no es primo pues solo posee un divisor y el 2 es el único primo par (solo divisible por 1 y por sí mismo). Aquellos números que tienen más de dos divisores se llaman compuestos, caso del 9 que presenta tres divisores 1, 3 y 9. Dada la aleatoriedad que muestra la secuencia de los números primos, la búsqueda de formas para determinar su comportamiento es uno de los retos no resueltos en Matemática, de ahí el juicio externado por Erdos.

La zarandade los números primos
En el siglo III a.C., el matemático, astrólogo y geógrafo griego Eratóstenes de Cirene propuso una forma, más pedagógica que matemática, para identificar los números primos entre cero y un valor “n”. Es un algoritmo que permite, de forma metódica, diferenciar los números primos de los compuestos. Por su comportamiento Eratóstenes le llamó criba, pues al igual que una zaranda o cedazo, permite separar ambas clases de números y dejar al descubierto solo los números primos. Esta herramienta es conocida como La criba de los números primos de Eratóstenes (o simplemente la Criba de Eratóstenes).
La criba de colores
Existe una versión muy atractiva de la Criba de Eratóstenes conocida como la Criba de colores. Además de ayudarnos a identificar los números primos, esta herramienta pedagógica nos ofrece toda una propuesta resumida sobre Teoría de números.
Vamos a construir la criba de colores para los números del 1 al 100. Iremos paso a paso hasta que el algoritmo nos depare la respuesta pretendida; luego buscaremos formas de obtenerle provecho.
Paso 1. Coloquémoslos números del 1 al 100 en una cuadrícula (zaranda) de 10 x 10.
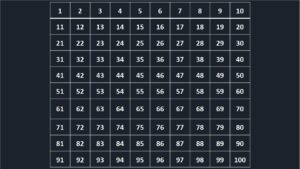
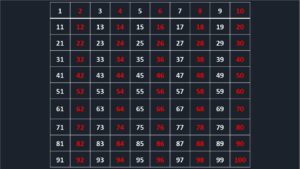
Paso 2. Manchemos en rojo los números pares (múltiplos de 2) y dejemos en blanco los impares
Forma o comportamiento: Observe como los números pares e impares se ubican en columnas perpendiculares, paralelas entre sí. Los pares, en rojo, terminan todos en 0, 2, 4, 6 u 8. Los impares, en blanco, terminan en 1, 3, 5, 7 o 9.
Paso 3. Bordeemos con un rectángulo celeste b a los múltiplos del3.
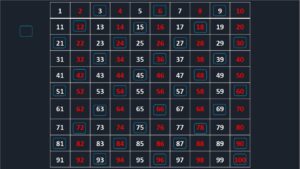
Forma o comportamiento: Los múltiplos del 3 se ubican en columnas oblicuas, paralelas entre sí, y la suma repetida de los dígitos que forman cada número siempre es 3, 6 o 9. Ejemplo, el 78, 7 + 8 = 15, 1 + 5 = 6.
Paso 4. Con un triángulo amarillo encerremos cada múltiplo del 4.

Forma o comportamiento: Los múltiplos del 4 son los múltiplos del 2, pero uno de por medio.
Paso 5. Con un círculo verde envolvemos a los múltiplos del 5.

Forma o comportamiento: Los múltiplos del 5 se ubican en dos columnas perpendiculares, paralelas entre sí, y todos los números terminan en 5 o 0. Ahora podrás entender por qué 35 470 o 482 065 son múltiplos de 5.
Paso 6. Con un signo de multiplicación “X” color gris, en la parte superior derecha, marcamos a los múltiplos del 6.

Forma o comportamiento: Los múltiplos del 6 son los múltiplos del 3 (bordeados por rectángulos celestes), pares.
Paso 7. Colocamos un menos“-“ color marrón en la parte inferior izquierda de los múltiplos del 7.

Forma o comportamiento: Número interesante que no muestra comportamiento preciso.
Paso 8. Con un corazón color papaya en la parte superior izquierda identificamos a los múltiplos del 8.

Forma o comportamiento: Los múltiplos del 8 son los múltiplos del 4, pero uno de por medio.
Paso 9. Un signo de suma“+” color fucsia en la parte inferior derecha identifica a los múltiplos del 9.

Forma o comportamiento: Los múltiplos del 9 se ubican en dos columnas oblicuas, paralelas entre sí, y la suma repetida de los dígitos que forman cada número siempre es 9. Es el caso del 99, donde 9 + 9 = 18, y 1 + 8 = 9.
La criba está concluida. Exceptuando 2, 3, 5 y 7 que presentan “mancha original”, los números en blanco y sin mancha, son todos primos. Caso del 29, 53, 67 o 97, entre otros. En total son 25 los números primos entre 0 y 100, lo cual se puede observar al tapar los compuestos y el uno.
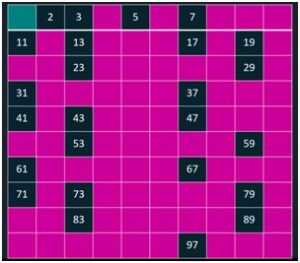
La criba de colores sintetiza la Teoría de números y es una excelente opción para hacer ejercicios lógicos. Pero ello será tema de un próximo artículo.