Mario Arguedas, profesor de matemáticas jubilado.
“Las matemáticas consisten en probar lo más obvio de la manera menos obvia.” George Pólya.
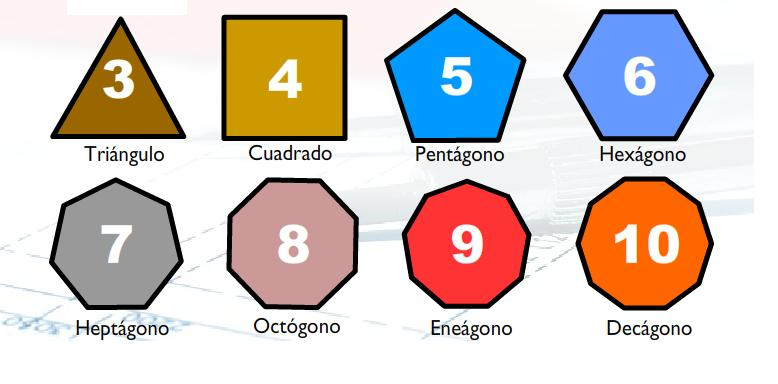
En atención a las medidas de los lados y a la abertura de sus ángulos internos, los polígonos pueden clasificarse en dos grandes familias:
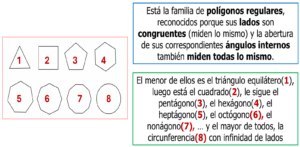
En contra posición encontramos a la otra gran familia, la de los polígonos irregulares o NO regulares, que no cumplen con alguno o ninguno de los dos requisito señalados para los regulares.
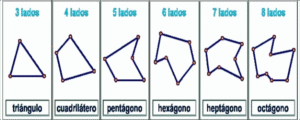
En este artículo analizaremos cómo determinar el área de las superficies correspondientes a los polígonos regulares (con infinito número de lados) y como ello se fundamenta en el área de superficies rectangulares. Iniciemos recordando lo ya dicho en otros artículos.
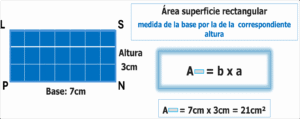
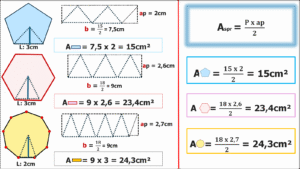
Tres ejemplos nos grafican la relaciónmencionada y nos muestran la forma del área de toda superficie poligonal regular.
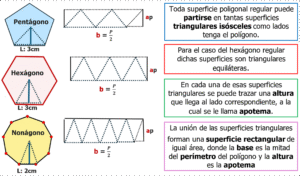
Puede entonces deducirse que el área de toda superficie poligonal regular está dada por el producto de su semiperímetro por la medida de una de sus apotemas (todas miden lo mismo) o como nos han dicho siempre, perímetro por apotema dividido por dos.
El infinitamente mayor
La circunferencia, concebida como un polígono regular de infinito número de lados, muestra al círculo como su correspondiente superficie poligonal,influenciado consecuentemente por la posibilidad de partirse en infinidad de superficies triangulares que unidas forman una superficie rectangular cuya área es el producto de la medida de la base(mitad del perímetro) por la de la correspondiente altura (asunto ya analizado en el artículo Las dos caras de la moneda), donde este último segmento llamado apotema, resulta ahora ser un radio del círculo.
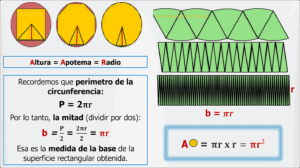

En este grupo el círculo se muestra como caso especial con un perímetro que corresponde a la circunferencia (2πr), la apotema se transforma en radio con medida r, para presentarnos su forma final clásica: ᴫr²(3,14 por radio al cuadrado).

Concluimos entonces que, en esencia, las áreas de las superficies poligonales presentan la forma de: medida de la base por medida de la altura.