Mario Arguedas, profesor jubilado.
«La esencia de la Matemática es su libertad». Georg Cantor

En un artículo anterior analizamos la relación circunferencia – diámetro y con ello el surgimiento de la constante ᴫ(PI) y su impacto en la obtención del perímetro de cualquier circunferencia, descrita en la forma:
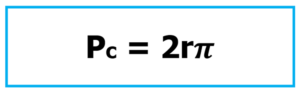
Que textualmente se lee: Perímetro de una circunferencia es igual a dos veces la medida del correspondiente radio (equivalente a la medida del respectivo diámetro) porᴫ
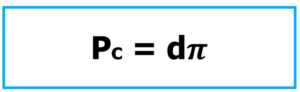
Pues bien, vencido el problema de la obtención de la medida de la circunferencia y descubierta por derivaciónla constante ᴫ,surge el problemasobre ¿cómo determinar la medida del círculo (superficie circunferencial)?
Primero aclaremos algunos conceptos que, ante la ausencia de rigor, tienden a interpretarse inadecuadamente:

Notas importantes:
1.La circunferencia NO tiene interior, le corresponde un interior.
2.La circunferencia, el diámetro y el radio están contenidos en el círculo.
- La circunferencia no tiene diámetro, ni radio; le corresponden diámetros y radios.
4. El perímetro de la circunferencia es su medida, por lo tanto, es lineal (en cm, dm, m, …).
- El área del círculo es su medida (número de superficies cuadradas que caben en la superficie circular), por lo tanto, se da en cm²,dm²,m²…
Y el punto 5 es el que plantea el problema por resolver: Encontrar una forma (manera o estrategia general) que permita determinar el área de un círculo, es decir, establecer con precisión el número de superficies cuadradas que caben en el círculo.
Una moneda, dos caras
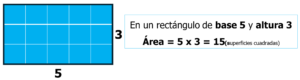
Determinar el área de una superficie rectangular no suele presentar mayor problema, pues los lados son segmentos de recta. La forma es el producto de la medida de la base por la medida de la altura.
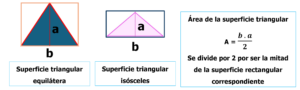
Tampoco presenta mayor problema determinar el área de una superficie triangular, sobre todo si corresponde a un triángulo equilátero (tres lados congruentes) o isósceles (dos lados congruentes), pues toda superficie triangular es la mitad de una superficie rectangular de igual base y altura.
Pues bien, en un acto de entera libertad, Arquímedes (287 a 212 a.C.) utilizó de manera empírica un principio del cálculo infinitesimal (conocimiento que se va a consolidar más de mil quinientos años después) para acercarse a la forma de obtener el área de un círculo.
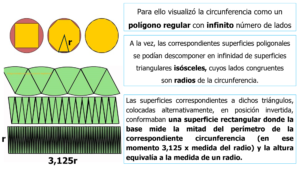
Por lo tanto, el área del círculo quedó bajo la forma del área de una superficie rectangular de base (3,125r) y altura r, lo cual se escribe:

Con el correr de los años, consolidados los conceptos sobre el valor deᴫ,las potencias y el cálculo infinitesimal, esa forma se muestra rejuvenecida como:
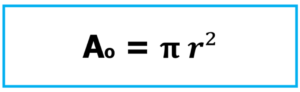
De esta manera perímetro de la circunferencia y área de la correspondiente superficie (círculo) identifican valores que en ambos casos comprometen al radio o diámetro y a la constanteᴫ.

Obsérvese como, para resolver la situación del área del círculo, la Matemática cambió, de manera arbitraria pero razonada, la concepción inicial de circunferencia, pasando de describirla como un conjunto de puntos en un plano equidistantes a un punto origen, para mostrarnos otra cara de la misma moneda al concebirla como un polígono regular de infinito número de lados. La primera permitió encontrar el perímetro de una circunferencia, la segunda favoreció la obtención de la forma del área del correspondiente círculo.



