Mario Arguedas, profesor de Matemáticas jubilado.
«La Geometría se ocupa de la relación lógicaque guardan sus conceptos entre sí». Albert Einstein.
El estudio de los cuadriláteros compromete el análisis de la forma del área de las superficies correspondientes a los trapecios. Para ello partiremos del área de las superficies rectangulares.
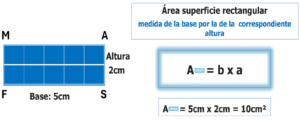
Los trapecios son cuadriláteros que tienen una única pareja de lados paralelos y como veremos el área de sus correspondientes superficies también presenta la forma de la una superficie rectangular:(medida de la base) por (medida de la altura).
Iniciemos observando el trapecio rectángulocuya característica particular es que presenta un ángulo interior recto (su abertura mide 90°).
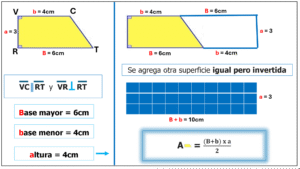
El área de la superficie trapecial rectangular es el producto de la medida de la base mayor más la de la base menor, por la altura correspondiente, todo dividido por dos.
La división por dos obedece a que, en la transformación, para obtener la superficie rectangular, se agrega una superficie trapecial rectangular igual pero invertida. Entonces, el área de la superficie VCTR es:
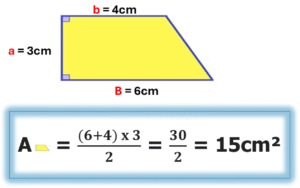
Ahora analicemos el trapecio isósceles ,cuya característica particular es que sus dos lados no paralelos son congruentes (miden lo mismo).
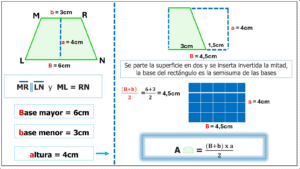
Como puede verse, el área de la superficie trapecial isósceles también resulta ser el producto de la medida de la base mayor más la de la base menor, por la altura correspondiente; todo dividido por dos.
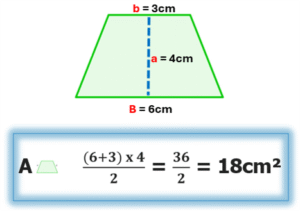
Por último corresponde el turno al trapecio escaleno cuya característica particular es que NO es rectángulo (no tiene ángulo interno recto), ni isósceles (sus lados no paralelos tienen diferente medida).
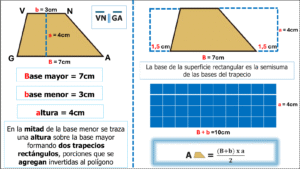
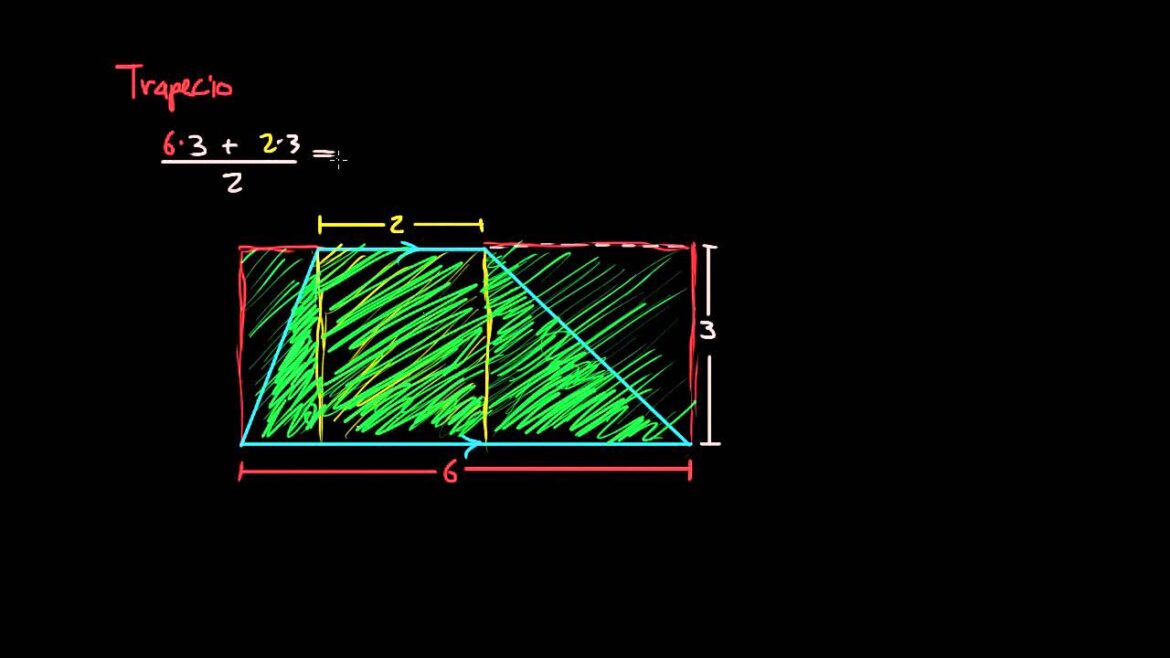
El ejemplo nos permite concluir que el área de la superficie trapecial escalena también resulta ser el producto de la medida de la base mayor más la de la base menor, por la altura correspondiente; todo dividido por dos.
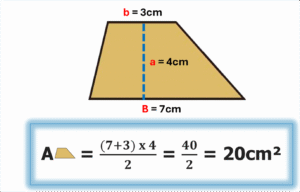
Por lo tanto, el área de toda superficie trapecial (rectangular, isósceles o escalena) siempre es el producto de la medida de la base mayor más la de la base menor, por la altura correspondiente; todo dividido por dos. Y como se logra ver, se explica con fundamento al área de una superficie rectangular.