Mario Arguedas, profesor jubilado.
“Cuando las leyes de la Matemática se refieren a la realidad, no son ciertas; cuando son ciertas, no se refieren a la realidad”. Albert Einstein.
Trabajar durante 5 días 8 horas diarias no es lo mismo que trabajar durante 4 días 10 horas diarias; pero en Matemática es verdad absoluta que 5 x 8 = 4 x 10 = 40.
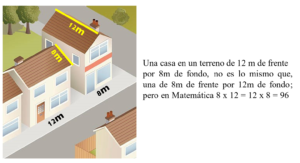
En ambos casos los ejemplos nos muestran una situación que tiende a presentarse en la enseñanza de las matemáticas escolares, como es el caso de dar por un echo que los estudiantes interpretan correctamente ciertas conclusiones o expresiones que ostentan alguna excepción o distorsión en su contenido. Por ejemplo, es preciso aclarar que, como operaciones, 5 x 8 y 8 x 5, no son iguales; sus productos (resultados) sí. Lo mismo sucede con 12 x 8 y8 x 12.
Brindar expresiones que no son correctas o dar por absolutamente ciertas conclusiones que en el fondo muestran alguna relatividad, creyendo que los estudiantes están interpretando bien lo que se dice, aunque parezcan nimiedades, son muestra de una ausencia de rigor en la enseñanza de las matemáticas y posiblemente una de las causas de deficiencias en sus aprendizajes.
El rigor en la enseñanza de las matemáticas es elemento constitutivo, obviarlo es desvirtuar una de las razones de la presencia de esta disciplina en la educación. Este hecho puede que se presente por un erróneo criterio de asociar rigor con dificultad o laboriosidad, y por ello rechazarlo. También puede ser por desconocimiento de la trascendencia del rigor matemático en la formación integral del estudiante, en cuyo caso sería muy lamentable.
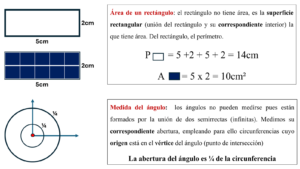
Verdades a medias
¿Una verdad a medias es una mentira, o una media mentira? He aquí algunas otras “medias verdades” en Geometría:
Una herencia fraccionada
En el campo de las fracciones las omisiones son frecuentes y a ello hay que abonarle un exceso de leguaje, lo cual presenta a éste como uno de los campos que presenta muchas deficiencias en su aprendizaje.

- Que ½ es mayor que ¼ es un precepto relativo, nunca absoluto. Dependerá de que se esté refiriendo a dichas fracciones aplicadas a una misma Unidad de Referencia (UR).
Las fracciones representan valores relativos, su cuantía depende de la respuesta a una pregunta clave, ¿de qué? (conjunto donde se proyecta la fracción),o, ¿de cuántos?(cantidad de elementos de dicho conjunto). Es verdad quela mitad de 100(50) es menor quela cuarta parte de 1000 (250).
Establecer con claridad el Conjunto Universo (¿de qué?) y la Unidad de Referencia (¿de cuántos?) favorece la ejecución con acierto de relaciones de orden (la triada mayor, menor e igual qué), así como la resolución de operaciones y problemas asociados.
Niccolò Tartaglia (matemático italiano del siglo XVI)planteó un problema que pone en evidencia la importancia de la Unidad de Referencia cuando tratamos con fracciones. Esta es mi versión:
Ante una oferta tan generosa, los hermanos aceptaron con beneplácito, quedando la distribución así:

Con este cambio en la Unidad de Referencia todos quedaron satisfechos, pero el abogado aún más. Los hermanos no tuvieron que partir ningún caballo y mejoraron lo contemplado en la herencia. Y lo impensable para ellos, el abogado recuperó el caballo donado y se ganó una plata adicional pues,9 + 6 + 2 = 17, por lo tanto, de la nueva UR sobró un corcel.
La Unidad de Referencia equivale al denominador común, un concepto que tiende a no comprenderse y sobre el cual se dicen algunas “verdades a medias”, como “que debe ser el mínimo común múltiplo de los denominadores”, “o cualquier múltiplo de los denominadores”, cuando lo cierto es que “puede ser cualquier número”. ¿O no?




