Mario Arguedas, profesor jubilado.
«Las abejas, en virtud de una cierta intuición geométrica, saben que el hexágono es mayor que el cuadrado y que el triángulo, y que podrá contener más miel con el mismo gasto de material». Pappus de Alejandría, matemático griego. 
La construcción de las colmenas o panales(*) por parte de las laboriosas abejas, constituye ejemplo claro de eficacia (dar respuesta precisa a una situación) y eficiencia (hacer uso maximizado de los recursos), al lograr almacenar una mayor cantidad de miel mediante el uso de menor cantidad de recursos.
El secreto está en la geometría de las estructuras y particularmente en la forma hexagonal de las celdas. Esta peculiaridad favorece el hecho de lograr, con polígonos que tienen igual medida, emplear aquel que encierra una mayor área(máxima superficie), sin dejar espacios huecos. ¿Cómo funciona ello? El desarrollo de este apartado busca explicarlo.
(*) En geometría, un panal es un empaquetado de poliedros o celdas que llena el espacio de modo que no quedan huecos.
De lo grande a lo amplio
Considere los rectángulos ABCD y PSTR, con sus correspondientes medidas:
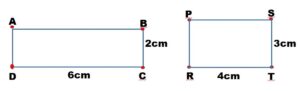
Dado que el perímetro es la medida del polígono (o sea la distancia que se recorre al dar una vuelta a la figura conformada por segmentos de recta), se puede concluir que:
Perímetro de ABCD = 16cm
Perímetro dePSTR= 14cm
- Por lo tanto, el rectángulo ABCD es más grande que el rectángulo
Perímetro de ABCD = 16cm
Perímetro de PSTR= 14cm
- Por lo tanto, el rectángulo ABCD es más grande que el rectángulo
Asociado a cada polígono hay un interior (parte del plano dentro del polígono, en este caso rectángulo) y un exterior (parte restante del plano). Ambas porciones del plano (interior o exterior) NO forman parte del rectángulo o polígono. Lo correcto es decir, interior o exterior que le corresponde al rectángulo o polígono.
La unión del rectángulo (o polígono) con su correspondiente interior, se denomina superficie rectangular (o superficie poligonal).

Toda superficie poligonal, aunque está formada por un conjunto infinito de puntos, es una porción limitada de un plano, situación que la hace susceptible de ser medida.
Para medir una superficie poligonal se utilizan porciones de plano que se toman como unidades de medida. Por ejemplo, en la sala de una casa donde el piso es de cerámica, cada pieza puede considerarse como unidad de medida de la superficie de la sala, indicando que la sala (superficie) mide “n” piezas. En este caso la unidad de medida utilizada es arbitraria, pues responde a un criterio personal.

En atención al Sistema Internacional de Unidades (SI),en la medida de superficies se utilizan como unidad es el metro cuadrado, sus múltiplos (decámetro, hectómetro o kilómetro, cuadrados) o submúltiplos (decímetro, centímetro o milímetro, cuadrados). Así, por ejemplo, un centímetro cuadrado es una superficie cuadrada de 1 cm de lado.
Determinar la medida de una superficie poligonal en centímetros cuadrados implica establecer cuántos de ellos caben o cubren la superficie en referencia. A ello se le denomina área de la superficie poligonal.
Si se consideran las superficies rectangulares ABCD y PSTR, con sus correspondientes medidas, se obtiene que:
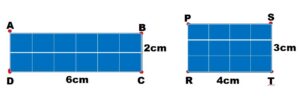
Área de superficie ABCD= 12 cm² (12 cuadrados de 1cm de lado)
Área de superficie PSTR= 12 cm² (12 cuadrados de 1cm de lado)
- Por lo tanto, las áreas son iguales
Entonces, se puede concluir que, figuras (polígonos) de diferentes tamaños pueden tener correspondientes superficies de igual tamaño, y esta es la razón intuitiva por la que las abejas se inclinan por celdas hexagonales.
Las abejas y su razón
Se procederá ahora a darles la razón a las geómetras de la naturaleza: las abejas.
Hay tres polígonos regulares (congruencia de lados y ángulos internos) cuya forma los distingue de los demás: el triángulo equilátero, cuadrado y hexágono regular. A ellos se le puede adicionar la circunferencia concebida como polígono regular de infinito número de lados.
Dichos polígonos gozan de una especie de perfección en su forma, pues su estructura presenta la peculiaridad de lograr áreas de mayor tamaño encerradas en perímetros de menor tamaño.
Dicha singularidad es utilizada por las abejas en la construcción de las celdas de sus colmenas, quienes durante su evolución han dominado el arte de almacenar la mayor cantidad de miel mediante el uso de la menor cantidad de recursos, al utilizar la forma hexagonal en sus panales.
El matemático griego del siglo IV, Pappo de Alejandría (más conocido como Pappus), fue el primero en preguntarse el por qué las abejas se decantaron por guardar la miel en hexágonos regulares, llegando a determinar que, al construir celdas hexagonales regulares, las abejas logran obtener áreas mayores a las de otras formas que tengan igual perímetro, lo cual les permitealmacenar hasta un 30% más de miel que si usaran otras formas.
Considérese como ejemplo un caso particular con las cuatro superficies regulares conocidas (se incluye a la circunferencia) y ubiquémoslas en una misma condición de tamaño (perímetros iguales):
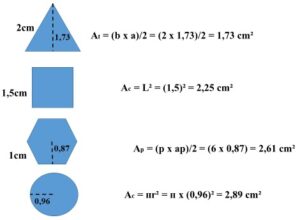
P = 3 x 2 = 6cm
P = 4 x 1,5 = 6cm
P = 6 x 1 = 6cm
P= 1,91 x ᴨ = 6cm
Obsérvese que los perímetros en los cuatro casos son iguales. Ahora véanse las áreas de las correspondientes superficies.
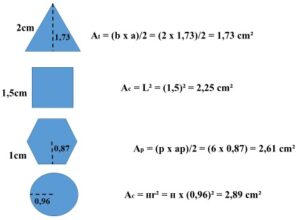
Es evidente que el polígono regular con una correspondiente superficie mayor es la circunferencia, pero si las abejas se decantaran por ellas, al unirlas quedarían cantidad de espacios huecos. Por ello construyen celdas de forma hexagonal regular, que, en su orden, cubren mayor superficie y se acomodan sin dejar espacios vacíos.
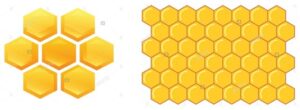
Se brinda así la razón a las pequeñas abejas, no sin antes destacar que, además de su don matemático, de su dulce miel y su oportuna cera, las abejas son vida, como lo señala el genio de la física Albert Einstein: “Si la abeja desapareciera de la superficie del globo, al hombre sólo le quedarían cuatro años de vida: sin abejas, no hay polinización, ni hierba, ni animales, ni hombres”.




