Mario Arguedas, profesor de Matemáticas jubilado.
«Donde hay materia hay Geometría», Kepler.
El filósofo italiano Giordano Bruno (1548-1600) refirió a la Geometría como “una de las nueve hijas de la Madre Musa que, junto a sus hermanas Aritmética, Música, Lógica, Poesía, Astrología, Física, Metafísica y Ética, explican el universo y la presencia del ser humano en él.” Y es que en sus orígenes la Geometría mostró un carácter eminentemente práctico e inmediato, tal y como lo dejan versus raíces etimológicas: Geo (tierra) y metrom (medida).

Sin embargo, en la Grecia Clásica el enfoque del conocimiento geométrico dará un sustancial giro en gran parte gracias a los trabajos del ilustre matemático Euclides (325- 265.AC), quien en su obra Los elementos, ordena el conocimiento geométrico y lo dota a la Matemática de generalización al demostrar sus verdadesbajo una lógica formal que hará de este saber, ciencia del pensamientoy por lo tantode verdades absolutas.

Esta dualidad en el enfoque (práctico-formal) de la Geometría, fue evidenciada por el prestigioso polímata francés Henri Poincaré (1854-1912) quien la describió como: “el arte de pensar bien y dibujar mal.”
Un asunto de estatura

El tamaño de un polígono lo determina la suma de las medidas de los segmentos que lo forman. Es una medida, un número y se llama perímetro.
El perímetro, desde una óptica visual, equivale al recorrido de una vuelta completa alrededor del polígono, que se puede hacer saliendo de uno de los vértices, pasando por los demás para llegar de nuevo al punto de salida.
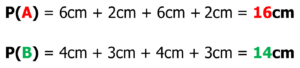
En acuerdo a este criterio, el rectángulo A es más grande que el rectángulo B, pues su perímetro es mayor.
Un asunto de superficies

Las superficies poligonales se miden con porciones de superficies tomadas como unidades de medición. De manera universal se emplean superficies cuadradas, por lo tanto, la medida de una superficie poligonal es el número de superficies cuadradas que le cubren. A dicho número se le denomina área de la superficie.
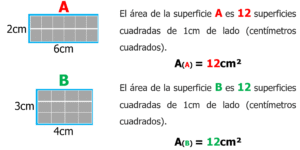
Como puede observarse:
- El rectángulo A es más grande que el B, pues su perímetro es mayor.
- La superficie rectangular A y la B miden lo mismo, pues sus áreas son iguales.
- El perímetro es la suma total de las medidas de los segmentos que forman el polígono (en este caso el rectángulo)
- El área es la cantidad de superficies cuadradas que “caben” en la superficie poligonal (en este caso rectangular).
- El perímetro y el área son medidas y por lo tanto números (pueden operarse).
- Lo correcto es perímetro del polígono (rectángulo) y área de la superficie poligonal (superficie rectangular).
- El polígono (rectángulo) no tiene interior y por lo tanto no tiene área, le corresponde un interior y consecuentemente un área.
Este último punto nos permite corregir algunas expresiones como es el caso de las diagonales, las cuales no pertenecen a los polígonos, sino a las superficies poligonales.
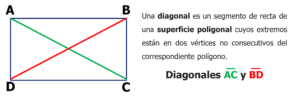
En este caso lo correcto es diagonal de la superficie rectangular ABCD, o correspondiente al rectángulo ABCD. De ninguna manera diagonal del rectángulo ABCD (incorrecto).
Área de superficies triangulares «Las matemáticas son el arte de dar el mismo nombre a diferentes cosas” , Henri Poincare. (1854 – 1912)
La forma de obtener el área de las superficies rectangulares constituye fundamento para determinar las áreas de las restantes superficies poligonales.
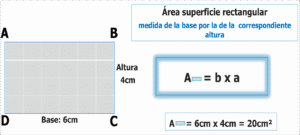
Es así como el área de superficies rectangulares nos permite obtener las estrategias para establecer el área de las siete variedades de superficies triangulares existentes:
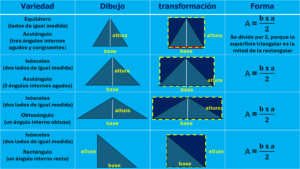
La estrategia es transformar las superficies triangulares en rectangulares agregando para ello una superficie triangular igual, razón por la cual la forma queda reducida al semiproducto (mitad del producto) de la medida de la base por lade la correspondiente altura. Lo mismo se aplica para las superficies asociadas a triángulos escaleno.
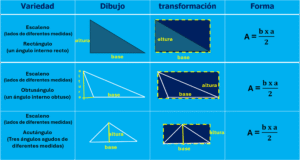
Algunas conclusiones pertinentes:
- La altura de una superficie triangulares un segmento cuyos extremos están, uno en un vértice y el otro en la base opuesta o su extensión (caso del triángulo escaleno, obtusángulo).
- La altura es perpendicular(forma ángulo recto) a la base o su extensión.
- Toda superficie triangular tiene tres alturas.
- La altura puede estar en el triángulo, caso de los triángulos rectángulos donde los catetos (lados perpendiculares) hacen las veces de alturas.En los demás casos la altura le pertenece a la superficie triangular, por ello lo pertinente es deciraltura correspondiente al triángulo.
- El área de toda superficie triangular es el semiproducto de la base por su correspondiente altura.
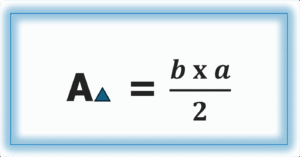
En próximos artículos me referiré a otras superficies poligonales y su relación con el área de las superficies rectangulares, pues como veremos todo se reduce a la forma b x a (medida de la base por la de la altura correspondiente). ¡Le espero!



