Mario Arguedas, profesor jubilado.
«El verdadero signo de la inteligencia no es el conocimiento, sino la imaginación». Albert Einstein
La siguiente pregunta puede resultar elemental: La suma de tres veces un mismo número es 12. ¿De qué número se trata? Es evidente que referimos al “cuatro”. Ahora replanteamos la pregunta así: La suma de tres veces un mismo número, que NO es cuatro, da 12. ¿De qué número se trata?
En la historia de las matemáticas se encuentran diversas situaciones como la planteada en el problema anterior, donde la estructura de pensamiento conocida, que da sustento, confiabilidad y solución, se ve sacudida por un cuestionamiento que, de pronto, no halla respuesta dentro del marco del conocimiento existente, provocando desconcierto.
La escuela Pitagórica (Grecia Clásica, siglo VI a.C.) vivió uno de esos desencuentros al comparar la diagonal y el lado de un pentágono regular, o la diagonal y el lado de un cuadrado. Por ejemplo, un cuadrado cuya medida de los lados fuese 1.
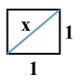
En atención al Teorema de Pitágoras la magnitud de la diagonal está determinada por la igualdad:
x² = 1² + 1²
x² = 1 + 1
x² = 2
x ‧ x = 2
Lo anterior porque el Teorema de Pitágoras establece que en todo triángulo rectángulo el cuadrado de la medida de la hipotenusa es igual que la suma de los cuadrados de las medidas de sus catetos.
Esta situación llevó a la interrogante, en apariencia elemental, de tener que encontrar “un número que multiplicado por sí mismo diera exactamente 2”.
x ‧ x = 2.
En ese momento de la historia los números conocidos eran los naturales y las fracciones o decimales, por lo tanto, los matemáticos hurgaron en ellos procurando encontrar la respuesta.
1 x 1 = 1
2 x 2 = 4
Tenía que ser un número entre 1 y 2 (un poco más cercano al 1):
1,41 x 1,41 = 1,9981.
1,4142 x 1,4142 = 1, 99996164.
Conforme anotaban nuevos decimales se aproximaban o pasaban de 2, pero no lograban encontrar un decimal que les llevara exactamente a él. De igual forma emergieron infinidad de preguntas similares, todas en apariencia sencillas, pero que no contaban una respuesta precisa.
X·X·X = 12 (¿qué número multiplicado por sí mismo tres veces da 12?)
X·X·X·X·X·X = 35 (¿qué número multiplicado por sí mismo seis veces da 35?)
Los Pitagóricos, agobiados por dichos planteamientos, optaron por dictar un precepto ,sustentado en un teorema de fácil demostración, el cual establecía que dichos números no existen y por lo tanto el problema no tenía solución. Y lo que no existe, se aparta, se olvida. Y ese olvido duró un poco más de 1 500 años.
Un Nuevo paradigma
La demostración de la NO existencia de los números en mención, se hace empleando el método de contradicción, que de forma resumida consiste en:
Partir del supuesto que ese número si existe, que es de la forma a/b (con a, b valores enteros, b 0) y en el desarrollo del proceso demostrativo surge una contradicción, un error, con lo cual se da por sentado que la premisa es incorrecta y por lo tanto el número buscado NO existe.
Una situación interesante es que, al querer demostrarse que esos números no existían y al hacerlo por el método de contradicción, se dejó entrever la posibilidad de que existieran. Y es aquí donde surge un segundo momento, allá por el siglo XI, posiblemente en la India (esta es opinión propia), donde algún matemático de los tantos destacados en esa época, sentenció:
Si el número que multiplicado por sí mismo no existe en el ámbito de los números conocidos (enteros o decimales), entonces habrá que inventarlo.
Lo anterior llevó a la invención de una nueva clase de números, unos que no eran posibles de representar en la forma a/b, un tipo de número cuyo cometido era ofrecer respuesta a lo planteado.
¿Qué número multiplicado por sí mismo da 5?
![]()
(que se lee raíz 2 o cuadrada de 5).
¿Qué número multiplicado por sí mismo 3 veces da 13?
![]()
(que se lee raíz tercera o cúbica de 13).
¿Qué número multiplicado por sí mismo 9 veces da 21?
![]()
(que se lee raíz novena de 21).
Este tipo de número surge, específicamente, para responder a la pregunta sobre “qué número, multiplicado por sí mismo “n veces”, lleva a un valor determinado”.
No había nada que demostrar, solamente inventarlos. De esta forma quedó resuelto el problema en referencia, con un altísimo nivel de rechazo por parte de los matemáticos occidentales de la época que vieron en dicha propuesta una forma fácil y nada convencional de responder a un hecho que no calzaba en el contexto hasta ahora conocido.

Propuestas como esta, de frecuente presencia en la historia de las matemáticas, motivaron al matemático húngaro – estadounidense John Von Neumann,a señalar que “las matemáticas no explican las cosas, sino que nos acostumbran a ellas”.
Cabe suponer que esta propuesta, en su momento tan descabellada, promotora del rompimiento de un paradigma más que milenario, además de hacer un aporte a las matemáticas, quizás contribuyó socialmente a imponer una norma de pensar hoy generalizada: lo que no se ha inventado aún, está para ser inventado, precepto este que, actualmente priva en la mente de científicos, técnicos, emprendedores o genios, o en el decir de los neófitos que con desenfado dicen “ahorita lo inventan o resuelven”.
No será hasta siglos después (por ahí del S.XVII) que los matemáticos, luego de pensarlo mejor, emplearon este conocimiento para dar solución a ecuaciones de grado superior a uno y, como es frecuente en matemáticas, el nuevo conocimiento, al aceptarse, estudiarse y consolidarse, de pronto encontró aplicaciones importantes en situaciones prácticas
Regresemos entonces a la pregunta inicial y busquemos darle respuesta a esa consulta:
La suma de tres veces un mismo número, que NO es cuatro, da 12. ¿De qué número se trata?
El “1”, porque: 11 + 1 = 12
Problema resuelto. ¿O no?



