Recuerda Sancho: la lengua queda y los ojos listos (El Quijote).
Los refranes son esos pensamientossurgidos con frecuencia en ambientes populares, cuyas expresiones encierran enseñanzas o moralejas. En lo personal los disfruto, sobre todo en forma de grafitis, quizá por la manera clara, precisa y concisa en que plantean las cosas, asunto que los semeja a las definiciones en matemáticas.

El refrán “lo que es bueno para el ganso lo es para la gansa” plantea un asunto de justicia al proponer igual trato para todos, en todo, esto en idénticas circunstancias.
En matemáticas yo encuentro que esta condición de equidad está presente en la relación e interpretación de ciertas cualidades para diversos entes matemáticos y que su análisis favorece principios de rigurosidad y objetividad. Revisaré algunos casos, iniciando con dos conocidos triángulos.
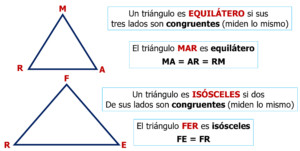
Equilátero o isósceles
De lo anterior se puede deducir que:
- El triángulo FER NO es equilátero pues presenta un lado (RE) no congruente con los otros dos.
2. El triángulo MAR, al ser equilátero es también isósceles, porque al tener tres lados congruentes cumple con la exigencia de tener dos.
3. Por lo tanto, todo triángulo equilátero es isósceles.
4. Por lo tanto, NO todo triángulo isósceles es equilátero.
5. Aunque el término equilátero alude a lados iguales, lo correcto es decir lados de igual medida.
- El término isósceles proviene de la raíz griega, iguales piernas. Desde esta óptica, el triangulo equilátero, al tener tres piernas iguales, tiene dos, por ello es isósceles, pues lo que es bueno para el ganso …
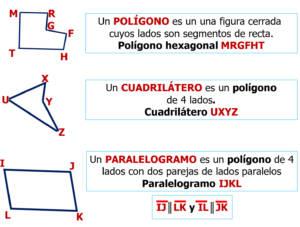
Polígono, cuadrilátero o paralelogramo. Veamos un segundo caso:
De lo propuesto se puede derivar que:
- Todo cuadrilátero es un polígono, pero no todo polígono es cuadrilátero.
- Todo paralelogramo es cuadrilátero, pero no todo cuadrilátero es paralelogramo.
Secuencia de paralelogramos. Continuando con este análisis consideremos tres paralelogramos muy conocidos: el rectángulo, el rombo y el cuadrado.
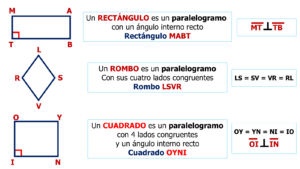
De lo expuesto se puede concluir que:
- Los tres polígonos son cuadriláteros (tienen 4 lados).
- Los tres polígonos son paralelogramos (tienen dos parejas de lados opuestos paralelos)
- El rectángulo MABT, no es rombo ni cuadrado (sus lados no son congruentes)
4. El rombo LSVR no es rectángulo ni cuadrado (no tiene ángulos internos rectos)
5. El cuadrado OYNYes rectángulo y rombo (lados congruentes y al menos un ángulo interno recto)
Por lo tanto, todo cuadrado es cuadrilátero, paralelogramo, rectángulo y rombo, pues cumple con los respectivos requisitos, y lo que es bueno para el ganso ….



